教員・研究室

ほとんど全ての物理現象は微分方程式としてモデル化・抽象化されます。しかし「シュレディンガー方程式、ディラック方程式、ナビエ・ストークス方程式などの物理学的に由緒正しい方程式には解が在って当たり前か？」となると、話はそう単純ではありません。物理現象を記述しているのは方程式の「解」であって「方程式そのもの」ではありません。「方程式そのもの」は書き下した瞬間「存在する」と言えるのでしょうが、方程式の「解の存在」は全く次元の異なる話題となります。また、「解の公式・具体的表示」と「解の存在」とは異なる概念です。後者は前者よりも広い意味を持っています。例えば、複素函数論で「複素係数のn次多項式は重複を許して丁度n 個の根を持つ」というガウスの代数学の基本定理を学びますが、これは「5 次以上の方程式は代数的には解けない」というアーベル・ガロアの理論とは何ら矛盾するものではありません。

さて、それでは「解の存在」とは何を意味するものなのでしょうか？そのためには、まず「解の概念」を明確に定義し、その上で「解の存在証明」を与える事が必要です。では何をもって「存在する」事を証明すれば良いのでしょうか？我々はその手段を解析学、特に函数解析学、調和解析学に求めます。そうなると、元来物理学から現れた偏微分方程式といえども、数学的対象として考える限り、徹頭徹尾数学的に扱わねばなりません。物理学的直感は役に立つ事もありますが、それを的確な数学的表現に置き換える作業が求められます。その様な思考過程の修業を経て初めて、物理現象の「数学的実在」が実感できるようになります。

「数学的実在」とは目に見えないものですが、確かに実感できるものであり、数式などの記号を用いて自由に表現する事のできるものです。それは同時に、自分の個性の表現でもあり、自己の実現・実在を強烈に感じる機会を与えてくれるものです。

小澤研究室は、物理と数学が交錯する場であると共に、志の高い人間の思考が相互作用し、世界の最先端の成果を発信する数理物理学道場を目指しています。
最後に現在取組んでいる課題と、対応する物理・応用物理の分野を並べて紹介します。

非線型双曲型方程式の研究　プラズマ物理、相対論、場の理論
非線型分散型方程式の研究　光通信工学、量子力学、場の理論
非線型楕円型方程式の研究　画像工学、材料工学、場の理論
流体力学の数学的基礎の研究　流体力学、連続体力学

古典力学、電磁気学、熱力学、量子力学、流体力学、連続体力学、光学、制御理論、相対性理論をはじめ、物理学科・応用物理学科で学ぶほとんどの理論系分野は微分方程式を理論の土台として体系化されています。

微分積分は力学や天文学とともに発展した歴史的経緯からも容易に想像されるように、数学的方法論は物理学の理解に欠かせない道具であり、物理学の発展を支える思考基盤となっています。
本学物理学科・応用物理学科には、物理学・応用物理学の理想的な学習プログラムが整備されており、世界最先端の研究が日々行われています。

本学物理学科・応用物理学科で数学と物理学の究極の世界を覗いてみませんか？

We cannot be assured of the validity of quantum field theory in any formulation without the deep mathematical theories drawn from the corresponding classical field theory.
In an address at the 1962 Conference on Analysis at Yale University on the occasion of Professor Hill’s retirement, Irving E. Segal remarked as follows: “To a considerable extent, relativistic physics is based in a theoretical way on non-linear partial differential equations. Until recently, however, there has been little applicable mathematical theory even in the classical (i.e., unquantized) case, although the subject is one of much intrinsic mathematical appeal. Probably the simplest non-trivial non-linear relativistic equations are those of the form 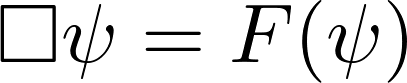, …” (from his paper entitled “Non-linear Semigroups,” Annals of Mathematics, 78(1963), 339-364.)
Given this common motivation, studies of nonlinear partial differential equations in classical field theory got their start as a subject in mathematical physics.
Up to the 1980s, the world’s leading centers of research in this area were located in New York and Paris.
The names of some of the prominent scientists working in this area immediately come to mind: Morawetz, Strauss, Nirenberg, Klainerman, Shatah in the U.S. and Jorgens, Lions, Ginibre, Velo, Choquet, and Christodoulou in Europe. In Japan, the first research group in this area took shape here in the Department of Applied Physics at Waseda University. Based on original and pioneering work by Professor Riichi Iino and Professor Masayoshi Tsutsumi, research results gradually percolated out into the world community during the 1980s.

Since then, the Mathematical Physics Laboratory, Department of Applied Physics, Waseda University has produced a number of mathematical physicists active in this area, including Nakao Hayashi, Yoshio Tsutsumi, Hayato Nawa, Takayoshi Ogawa, and myself, to name a few. Individuals active in these laboratories are now recognized as a world-leading group in the mathematical study of classical field theory.

I returned to Waseda in 2008 to succeed Professor Masayoshi Tsutsumi. With Professor Shigeaki Koike, I oversee the Laboratory of Mathematical Physics. My chief research interests involve classical field theory as a topic in mathematical physics. In terms of nonlinear partial differential equations, I have done work in the areas of nonlinear hyperbolic equations, nonlinear dispersive equations, and nonlinear elliptic and parabolic equations arising in pure and applied physics, particularly nonlinear Dirac, Klein-Gordon, Schrodinger equations, several associated systems of these equations, and fundamental equations in fluid mechanics. By exploring basic issues associated with these equations, such as the well-posedness of the Cauchy problem, long-time behavior of global solutions, regularity and singularity in local solutions, scattering theory, and asymptotic analysis, I seek to obtain a clearer picture of the mathematical reality of classical field theory. For more information, I encourage you to visit our Laboratory website.

Most of the theoretical fields studied in the Department of Physics and Applied Physics, including classical mechanics, electromagnetism, thermodynamics, quantum mechanics, fluid mechanics, continuum mechanics, optics, control theory, and theory of relativity, are systematized with differential equations as their theoretical foundation.

As can be easily imagined from the historical background in which differential and integral calculus developed alongside mechanics and astronomy, mathematical methodology is an essential tool for understanding physics and is the foundation of thought that supports the development of physics.

Our Department of Physics and Applied Physics offers an ideal study program for pure and applied physics, and world-leading research is conducted on a daily basis.
Why not take a peek into the ultimate world of mathematics and physics at our Department of Physics and Applied Physics?